1°- Criando o perfil envolvente da engrenagem
Imagem do livro Sarkis Melconian
Elementos de máquinas:
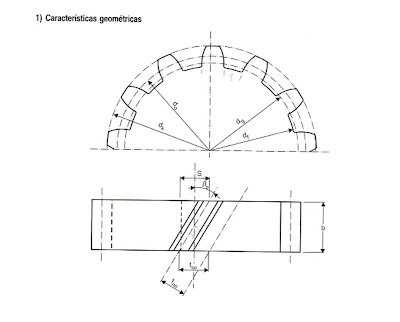 ts0 = passo frontal
ts0 = passo frontaltn0 = passo normal B0 = ângulo da hélice
alfa = ângulo de pressão normal
d0 = diâmetro primitivo
dk = de = diâmetro externo
df = di = diâmetro interno
dg = diâmetro de base
A postagem anterior temos uma imagem do livro cascilas ensinando a traçar o perfil da engrenagem, o que muda aqui são os diâmetros de uma engrenagem helicoidal, vamos calcula-los da seguinte forma:
Lembrando que o módulo normal, número de dentes, largura, ângulo de hélice, e passo normal já são dados conhecidos. Os dado aqui trabalhado são:
tn0 = 6,28; mn = 2; d0 = 61,72; dg = 57,6; di = 56,92; de = 65,72 ; z = 29 dentes;
B0 = 20° (ângulo da hélice) ; alfa = 20° (ângulo de pressão normal)
Espessura = tn0 / 2
Módulo frontal = Mn /cos(ângulo da hélice) ; onde mn é módulo normal
Ângulo de pressão frontal = arctg [tg(ângulo de pressão normal) / cos(ângulo da hélice)]
Do = z * módulo frontal
De = d0 + (2*hk) ; onde hk = mn
Di = d0 – (2*hf) ; onde hf = 1,2.mn
Criando o perfil no sketch do inventor:

Aplicando o comando circular pattern nos dois arcos envolventes da engrenagem. Usando o comando trim e eliminando o diâmetro primitivo e de base temos:
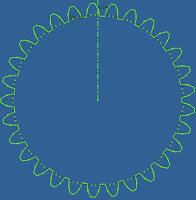 Antes de continuarmos as etapas precisamos entender o que é um passo, pois vai ser muito útil para o desenvolvimento do 3D.
Antes de continuarmos as etapas precisamos entender o que é um passo, pois vai ser muito útil para o desenvolvimento do 3D.2° - Passo
È todo percuso que resulta num ciclo, diferente do avanço onde este é um percurso que não necessariamente se repete.
Pelo que conhecemos existem quatro tipos de passos:
· Passo angular
· Passo senoidal
· Passo de circunferência
· Passo normal
Na verdade os outros dois passos são derivados do passo angular.
2.1- Passo angular
Vamos pensar num sextavado, seu passo circular é de acordo com seus lados

Onde alfa = ( 360 / n° de lados) , portanto alfa = 60°
2.2- Passo de circunferência
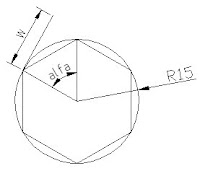 Corresponde ao comprimento do arco:
Corresponde ao comprimento do arco:Onde w ={ (2*raio*PI)/n° de lados} , portanto w = 15,7
2.3 Passo frontal
Esse é o mais usado, corresponde a corda do arco:
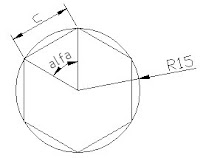 Onde c = { sen( 180 / n° de lados )* diâmetro ) ou c = { sen ( 180 / n° de lados ) * 2 * raio }, portanto c = 15
Onde c = { sen( 180 / n° de lados )* diâmetro ) ou c = { sen ( 180 / n° de lados ) * 2 * raio }, portanto c = 15Um passo muito importante para nós, do qual vai ser usado neste método de desenho 3D, é o da função seno ou coseno:
2.4 -Passo senoidal
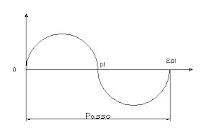
Onde o passo é o comprimento do percurso senoidal até completar um ciclo.
Agora que sabemos o que é um passo voltemos para nosso desenho.
3° - Conhecendo o passo de uma engrenagem:
O passo principal de uma engrenagem é o angular, pois estes corresponde a todos os passos normais nos diâmetros primitivo, de base, interno e externo, como se fosse de um sextavado dividimos 360° pelo número de dentes; este ângulo corresponde ao início da ponta do dente ao final da próxima:
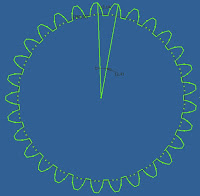 A partir deste passos angular finalizamos o scktch e aplicamos extrude somente nesta parte do passo ( podemos adotar uma espessura de 1 mm somente por referência) :
A partir deste passos angular finalizamos o scktch e aplicamos extrude somente nesta parte do passo ( podemos adotar uma espessura de 1 mm somente por referência) : 3.1- Criando uma linha de referência
3.1- Criando uma linha de referênciaSelecionamos sua lateral esquerda e aplicamos o comando scketch, sucessivamente delimitando uma linha de centro paralela a linha de largura que adotamos de 1mm (extrude), saindo do centro desta engrenagem para sua direita, de comprimento um pouco mais que a largura original da engrenagem e finalizamos o scktch (saberemos mais tarde o porquê desta linha):


4°- Usando o comando Circular pattern .
Depois de termos finalizado o scktch, aplicaremos o circular pattern para dar o formato da engrenagem (no nosso caso são 29 dentes) :

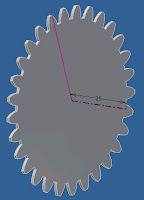
Criamos agora um scktch na face onde se localiza a linha de centro e finalizamos o scketch (pois o comando que vamos usar para rotaciona-la em forma helicoidal necessita deste passo):
 5° - Criando os dentes helicoidais.
5° - Criando os dentes helicoidais. Criacando no comando Coll, que fica na seção do extrude, revolver, hole, Shell, etc; vamos criar os dentes helicoidais,mas antes disto é preciso entendermos algumas coisas:
a) Quando olhamos frontalmente para uma engrenagem observamos que o dente anterior avança um pouco em relação ao dente da frente:
a = tg ( ângulo da hélice ) * largura da engrenagem, no nosso caso:
a = tg (20°) * 22,3 = 8,116
V = arccos{ ( 2*Re² - a² ) / ( 2*Re² ) }, no nosso caso v = 14,18°
Concluímos que para um avanço helicoidal ( a ) gerado pelo ângulo de hélice e a largura da engrenagem, conduzirá uma variação angular frontal,.
Com todos estes dados podemos conhecer o que chamamos de passo helicoidal.
5.1 - Passo helicoidal
O passo helicoidal é semelhante a um passo senoidal ( item 2.4), o ciclo completo é 360° ou 2pi, é como se imaginássemos a engrenagem girando sentido horário e avançando no eixo z (largura) ao mesmo tempo.
Assim, se v é menor que 360° esta variação angular frontal não deu uma volta completa, portanto, para sabermos o passo é necessário aplicarmos uma regra de três:
V -------- largura
360------Passo
Passo helicoidal = { ( 360 * largura da engrenagem) / V }
No nosso caso: Passo helicoidal = ( 360 * 22,3 ) / 14,18 = 566,149
Passo helicoidal = 566,149
Contudo, temos um problema ainda, quando usarmos o comando Coll, selecionamos a face pertencente a linha de centro (profile) depois selecionamos a linha de centro (Axis), não podemos clicar em Ok ainda, precisamos ir na aba ( coll size) em type iremos optar por Pitch and revolution ( Passo e voltas) e inserimos o passo helicoidal em pitch; agora precisamos saber a revolucion ( número de voltas)
5.2 Calculando o número de voltas
Se a variação angular frontal (v ) não ultrapassou 360°, significa que não completamos uma volta, então nossa revolution irá ser menor que 1, aplicando mais uma vez a regra de três:
1volta --------- 360°
Xvolta ---------- V
Xvolta = (v / 360), no nosso caso xvolta = (14,18/360) = 0,03938
Xvolta = 0,03938
Resumo:
· a = tg (ângulo da hélice ) * largura da engrenagem
· Passo helicoidal = { ( 360 * largura da engrenagem) / V } --> Pitch
· Xvolta = (v / 360) -> Revolution
Agora podemos dar a forma helicoidal para nossa engrenagem.
6° - Forma helicoidal

7°- Excluindo o plano que criamos
Em nossa peça observamos que uma parte continua plana, esta parte foi o plano que criamos de 1mm para construção de nosso desenho, basta selecionar o lado que esta planificado, aplicar e finalizar o scketch; com o comando extrude, ao invés de acrescentarmos material vamos cortar esta parte com o comando CUT dentro do formulário extrude .